Brillouin scattering is the physical effect used for sensing temperature and deformation. Brillouin interaction is illustrated in a simplified way in Figure 2: the Electro-Magnetic (EM) field of the lightwave injected in the fibre (pump light) has both electrical field (E) and magnetic field (B) components.
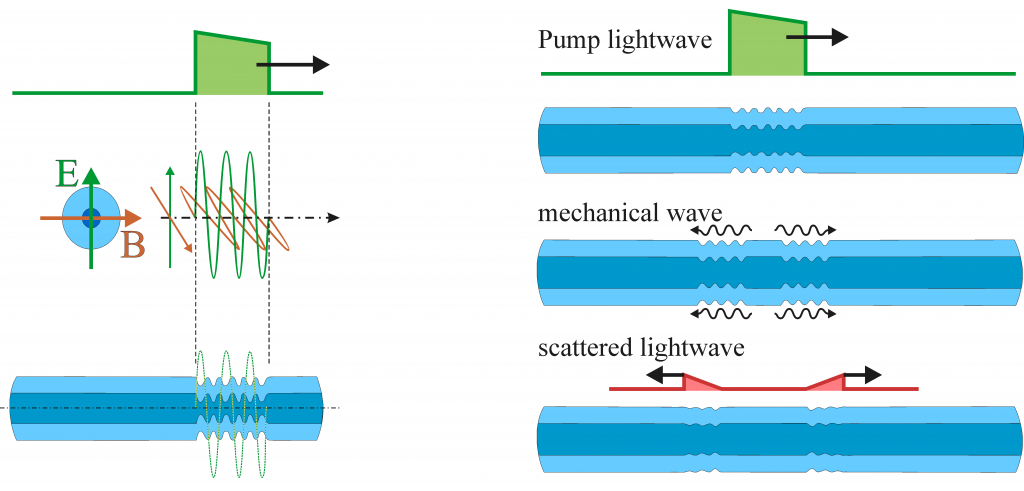
Figure 2: In Brillouin effect the light-waves (photons) interact with vibrational states of the fiber (phonons) changing the photon energy and changing the light wavelength (‘colour’)
When the lightwave (pump wave) propagates in a physical medium such as the glass of the fibre, the electrical field (E) interacts with the material by changing the material density through the electro-striction effect. The striction pattern then generates vibration waves (phonons), this at the expenses of the energy of the pump light that gets its energy reduced. The effect also implies that a vibration wave (phonon) which is present in the material interacts with the EM field through energy exchange. The mechanical deformation pattern interacting with the pulsed light (phonons) can survive only for a limited amount of time (a lifetime of the nanosecond order). This energy exchange between vibrations (phonons) and the optical pump EM field (photons) gives rise to generation of photons (EM waves) with different energies (frequencies), i.e. light-waves with wavelength (‘colour’) shifted with respect to that of the pump light. This is called the Brillouin effect.
The most likely Brillouin scattering process is the “Stokes” interaction in which the pump light looses energy in order to create the mechanical waves (phonons), and the scattered light thus results red-shifted (lower optical frequencies) with respect to the pump. A mirror process, in which a pump photon gets energy from a pre-existing mechanical wave (excited phonon) increasing the photon energy (frequency blue-shift) is as well possible although with lower probability, and it is named “anti-Stokes” Brillouin interaction.
In order to efficiently generate Brillouin scattering, the spectral purity combined with the intensity of the pump light must create a regular and strong pattern of electrostriction. This translates into some constraints on the pump lightwave in terms of maximum linewidth and minimum power threshold.
The Brillouin effect arises from a excitation/dis-excitation process in which some EM energy is temporarily stored in a shoert-lifetime mechanical form, and it can turn back into EM energy spontaneously, as well as a stimulated effect, i.e. consequentially to a “resonance” stimulus, in a conceptually similar way to other physical excitation/dis-excitation processes such as fluorescence and light amplification [1].
The characteristics of Brillouin scattering depend essentially on fiber glass properties (e.g. refractive index, density etc.). Since these are strongly influenced by optical fiber temperature and deformation, it is then straightforward that by measuring the fiber Brillouin scattering characteristics it is possible to reliably estimate the optical fiber temperature and deformation conditions.
[1] EP Ippen, RH Stolen, Stimulated Brillouin scattering in optical fibers, Applied Physics Letters, 21[5], p. 539, (1989).
